Sine and Cosine in Real Life

The earliest studies of triangles can be traced to the 2nd millennium BC, first as Egyptian Mathematics and Babylonian Mathematics. The first systematic study of trigonometric functions began in Hellenistic Mathematics.

Sine is one of the six fundamental circular functions of an angle. Etymologically, the word sine derives from a Sanskrit word jiva, in Arabic, jaib, meaning "bosom", "bay" or "chord". The word sine was first introduced in 1950's.

Sin(x) as graphed

Animation showing how the sine function (in red)  is graphed from the y-coordinate (red dot) of a point on the unit circle (in green) at an angle of θ in radians.

In Triangle, with angle θ, sine is calculated as:

sin(θ) = Opposite / Hypotenuse

In picture form: 

For the angle α, the sine function gives the ratio of the length of the opposite side to the length of the hypotenuse.

Cosine, is also one of the six fundamental circular functions. In fact, the sine and cosine functions are closely related and can be expressed in terms of each other.

The cosine definition basically says that, on a right triangle, the following measurements are related:

• the measurement of one of the non-right angles (q)
• the length of the side adjacent to that angle
• the length of the triangle's hypotenuse

Cos (x), as graphed

In triangle:

Relating in real life:

You might ask, "Why do we study this?" "Is this essential in real life?" Of course, yes. Sinusoidal waves (or sine waves for short) have turned out to be essential to understanding how our world works. 

One example is sound. You might not know that we use the sine and cosine functions while you play instruments, or listen to stereo. You listen to sound waves. We can think of these as having the shape of sine waves. For example, if you know anything about playing a piano, the note A above middle C produces a wave shaped like 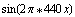. If you figure out the period of this function (using the theorem from class) you'll see that this wave has 440 complete cycles every second.

The graph of Note A: 

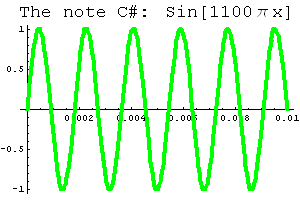
The graph of Note C#:

The graph of Note E:

But when you listen to your stereo sound, you hear a lot more. You hear  more than one note at a time. It's simple, it is the combination of the sine functions of the Note A, C#, and E. 

You can see that the graph is no longer as sine curve, but there is a pattern to it. And the pattern only repeats, so it is still a periodic function.