Surveying
 |
Graphing, can be used in illustrating bacterial growth (as I remember, we studied this)
 |
| Calculation of generation time |
he exactly doubled points from the absorbance readings were taken and, the points were extrapolated to meet the respective time axis.
Generation Time = (Time in minutes to obtain the absorbance 0.4) – (Time in minutes to obtain the absorbance 0.2)
= 90-60
= 30 minutes
Let No = the initial population number
Nt = population at time t
N = the number of generations in time t
Sine is also used in Pendulum Motion.
The position of the pendulum bob (measured along the arc relative to its rest position) is a function of the sine of the time.
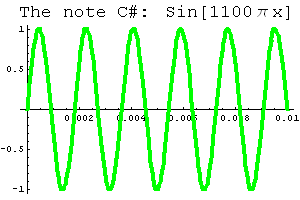
It is used in signal transmission, television, radio broadcasting involves waves described in sine/cosine.
 |
| Diagram of the electric fields (E) and magnetic fields (H) of radio waves emitted by a monopole radio transmitting antenna (small dark vertical line in the center). The E and H fields are perpendicular as implied by the phase diagram in the lower right. |
Many compression algorithms, like JPEG, GIF, JPG (and other picture formats) use fourier transforms that rely on sine and cosine. In fact most anything involving sound waves will rely on sin/cos. Space flight relies on calculations and conversions to polar coordinates. So do satellites. Ballistic trajectories rely on sin/cos, and there are numerous other uses of them in physics.